Legendre's conjecture
Legendre's conjecture, proposed by Adrien-Marie Legendre, states that there is a prime number between n2 and (n + 1)2 for every positive integer n. The conjecture is one of Landau's problems (1912) and remains unsolved.
The prime number theorem suggests the actual number of primes between n2 and (n + 1)2 (sequence A014085 in OEIS) is about n/log(n), i.e. about as many as the number of primes less than or equal to n.
If Legendre's conjecture is true, the gap between any two successive primes would be 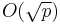 . In fact the conjecture follows from Andrica's conjecture. Harald Cramér conjectured that the gap is always much smaller,
. In fact the conjecture follows from Andrica's conjecture. Harald Cramér conjectured that the gap is always much smaller, 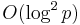 ; if Cramér's conjecture is true, Legendre's conjecture would follow. Cramér also proved that the Riemann hypothesis implies a weaker bound of
; if Cramér's conjecture is true, Legendre's conjecture would follow. Cramér also proved that the Riemann hypothesis implies a weaker bound of 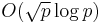 on the size of the largest prime gaps. Legendre's conjecture implies that at least one prime can be found in every revolution of the Ulam spiral.
on the size of the largest prime gaps. Legendre's conjecture implies that at least one prime can be found in every revolution of the Ulam spiral.
Legendre's conjecture follows from Oppermann's conjecture.